Maths Walking Tour
If you're keen to do some mathematics whilst sightseeing around Edinburgh, then our walking tour is for you.
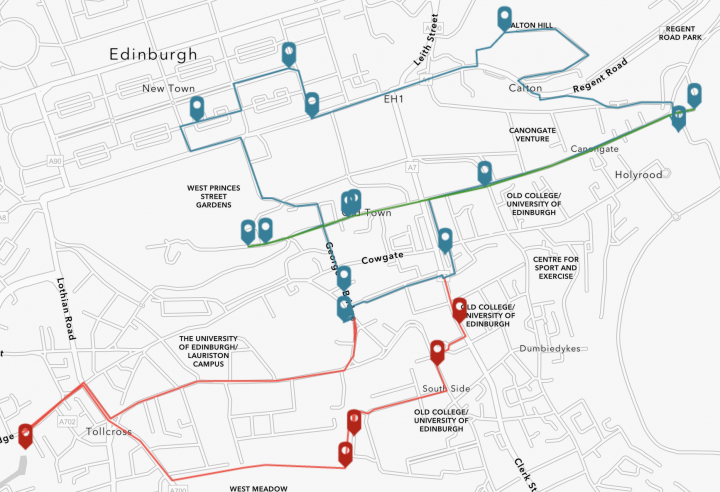
This page contains further information and directions for the Edinburgh Maths Walking tour we have created. For details about the various stops, and to try the fun and engaging puzzles, visit the walking tour webpage.
Directions
Green Route (1/2 hour - 1 mile/1.5km)
1) The Witches Well is located at the top of the Royal Mile at the east end of the Castle Esplanade, on the side of the Tartan Weaving Mill.
2) Walk down the Royal Mile to the Camera Obscura.
3) Cross over George IV Bridge/Bank Street and and walk on a little, to where you will find the Heart of Midlothian mosaic (outside the Cathedral), and the gold bricks marking the Luckenbooths.
4) Continue along the Royal Mile, heading downhill, where you will find The Worlds End on your right.
5) Head further along the Royal Mile until you reach the east/bottom end, where you will find the Scottish Parliament and Holyrood Abbey.
Blue Route (2.5-3.5 hours depending on stops/reading; can be walked in about 1.5 hours. 3.5 miles/6km)
1) The Witches Well is located at the top of the Royal Mile at the east end of the Castle Esplanade, on the side of the Tartan Weaving Mill.
2) Walk down the Royal Mile to the Camera Obscura.
3) To get to the Edinburgh Bow Tie Company, continue down the Royal Mile until you get to Bank Street (with Deacon Brodies Tavern on the left), and turn left. Continue straight on towards the Museum on the Mound and turn left onto North Bank Street. Follow this round to the right, across the crossroads onto The Mound, which continues northwards, downhill towards Princes Street. Cross the road and turn left, continuing until Frederick Street, where you will turn right onto it, and then right again onto Rose Street. The Edinburgh Bow Tie Company will be on your left.
4) Continue along Rose Street until you get to the first major crossroads with Hanover Street. Turn left (north) and continue until the junction with George Street (with the statue of George IV in front of you). Turn right onto George Street and continue east to the James Clerk Maxwell Statue, which is directly in front of St Andrew's Square.
5) Turn right onto South St Andrew Square/St David Street and continue downhill to Princes Street; you can see the Scott Monument in front of you.
6) Upon reaching Princes Street, turn left (east) and continue straight on, past the end of Leith Street, until you reach Howies Restaurant on your left. Cross the small road in front of you and continue for a few yards until reaching stairs on your left. Ascend the stairs and turn right onto another set of steps. Continue until you reach the top of Calton Hill where you will easily find the City Observatory.
7) Descend Calton Hill, by continuing east and taking Calton Hill Road, which loops down and back towards where you made your ascent. Alternatively, return via the steps and walk east towards the end of Calton Hill Road. Once you reach the junction of Calton Hill Road and Regent Road, continue east along Regent Road and cross to the other side. There are now a number of routes to Holyrood Abbey: i) [Shown on Map] Immediately on your right will be a small entry-way onto steps, which leads down a path onto Calton Road. OR ii) Continue along Regent Road, past the Burns Monument on your right, until you reach the entrance to New Calton Burial Ground. Make your way through the cemetery, heading south, where you will exit onto Calton Road. One you reach Calton Road, follow it east (turn left) until it reaches a roundabout; Holyrood Palace, and the Abbey, are straight ahead and to the right of you. OR iii) Follow Regent Road past New Calton Burial Ground, taking a path on the right next to a grassed area to Abbey Mount. Turn right and follow the road to the roundabout; Holyrood Abbey will be on your left.
8) The Scottish Parliament is directly across Horse Wynd from Holyrood Palace.
9) Take the Royal Mile (Canongate) and walk uphill (west). Continue until you find The Worlds End on your left. It is on the junction of the Royal Mile and St Mary's Street.
10) Continue up the Royal Mile until you reach Niddry Street on your left (between The Raddison and The Inn on the Mile). Turn left, taking Niddry Street downhill. Cross over Cowgate, heading straight on. The distrinctive door of The Oyster Club will be on your right.
11) Niddry Street is a dead end, so turn around, walk back Cowgate, turn right onto it, and then immediately right onto Robertson's Close. Continue uphill to Infirmary Street, and turn right where you will find South Bridge. If you want to complete the longer (red) route, then turn left along South Bridge and follow those instructions.
12) Cross South Bridge onto Chalmers Street and continue west, past the National Museum of Scotland, until you reach George IV Bridge. The statue of Greyfriars Bobby will be on the other side of the road. Cross the road, and head to the left of the statue into Greyfriars Kirkyard. Colin Maclaurin's memorial is on the south side of the Kirk. James Stirling's memorial is a small plate written in Latin, between two large tablets on a wall - can you find it?
13) Exit the Kirkyard where you came in, and walk left along George IV bridge (do not take Candlemaker Row, which is the smaller street heading downhill). The Elephant House, famous for Harry Potter, will be on your left, just before George IV Bridge crosses another street below it.
14) Continue along George IV Bridge until you reach the Royal Mile (this is where you turned left at the start of the walk). Turn right (east) onto the Royal Mile, and walk on a little, to where you will find the Heart of Midlothian mosaic (outside the Cathedral), and the gold bricks marking the Luckenbooths.
Red Route (+1 hour 2.5 miles/4km)
1) Starting from South Bridge/Chambers Street [Point 11 of the blue instructions], walk south along South Bridge/Nicholson Street, and Surgeons' Hall will be on your left.
2) Cross the road and go straight on (west) past Nicholson Square Gardens. The Bayes Centre is straight ahead of you on Potterrow.
3) Turn left along Potterrow until you reach Crichton Street (opposite the Mosque). Turn right onto it and continue along George Square, taking the passage straight on in front of the Chrystal Macmillan Building, towards Sainsbury's. Before reaching the bollards, turn left along George Square Lane. St Albert's Chapel is through a gate on your left.
4) Return along George Square Lane, turn left through the bollards and immediately left again onto Middle Meadow Walk. Continue straight on to The Meadows.
5) Once you enter The Meadows, turn right along Meadow Walk and continue (west) until the end of The Meadows. Turn right along Brougham Place and continue to the complicated crossroads. Head straight on, along Earl Grey Street until you reach Fountainbridge on your left. Turn left onto it and continue until you reach Akva on the left. Take the small passageway on your left and you will find the Canal Basin.
6) Return to Fountainbridge through the passageway and turn right, returning to Earl Grey Street, and turn right again. Now take the first left onto Lauriston Place. Continue for about 1/2 mile/800m, passing George Heriot's School on the left, until you reach Forrest Road on your left (opposite Middle Meadow Walk). Turn left onto it and continue until reaching Greyfriars Kirkyard on your left (just before the Greyfriars Bobby pub/statue). Continue from point 13 of the blue instructions.
Solutions
There are three strategies they could follow:
- Each could guess the same colour as her card;
- Each could guess randomly;
- One could guess the same colour as her card, the other can guess the opposite.
The first strategy means they will lose if they have the same colour cards, so a 50% chance.
For the second strategy, each witch has a ½ chance of guessing correctly, so their chance of guessing correctly is ¼, or 25%.
As for the third strategy, it turns out to be a winning strategy - they are released every time! These are the possible scenarios:
-
1 gets red, 2 gets red: 1 guesses red, 2 guesses black. 2 is incorrect and they are released.
-
1 gets red, 2 gets black: 1 guesses red, 2 guesses red. 1 is incorrect and they are released.
-
1 gets black, 2 gets red: 1 guesses black, 2 guesses black. 1 is incorrect and they are released.
-
1 gets black, 2 gets black: 1 guesses black, 2 guesses red. 2 is incorrect and they are released.
Why does this work?
The first player is guessing the colour she gets. In other words, she is only right if they both have the same colour card.
The second player, on the other hand, is guessing the opposite of the colour she gets. So, she is only correct if they have opposite colour cards.
This means that one of them is bound to be incorrect regardless of what colour cards they receive, and, with this strategy, both can live!
The two triangles are similar, and so we can use the fact that we know the dimensions of the larger one to determine the size of the smaller one. You could use Pythagoras’ Theorem to work out the missing side length of the big triangle, find the corresponding side of the small triangle (using that the sides of the large triangle are in the same ratio as those in the small one), and then find the horizontal distance, again using Pythagoras’ Theorem. However, a more elegant solution is to realise that the horizontal ‘widths’ of the two triangles have the same ratio as the vertical sides, so the distance to the wall is 80/60m = 4/3m.
This may seem impossible! The trick is to cross your arms before you pick the two ends of the scarf. In this way you tie a knot with your arms, and then “transfer” it to the scarf.
If you pick the two ends of the scarf as you would naturally do, without crossing your arms, your arms and the scarf would basically make a circle, and there is no way to knot a circle.
Image 1 is Red, image 2 Blue, and image 3 Green. One way to work this out is to notice that the wings are very blue (possibly with some green), and hence should be bright in the Blue image and very dark in the Red image. The Green image is then the remaining one.
The pigpen translates to “Oh, what a tangled web we weave when first we practise to deceive!”, from Walter Scott’s poem “Marmion: A Tale of Flodden Field”.
The speed of light in vacuum is c = 3 x 108 meters/second
So, light leaving Alpha Centauri would take (4.1315 x 1016)/(3 x 108 ) = 137716666.667 seconds
One year has: 365 days x 24 hours per day x 60 minutes per hour x 60 seconds per hour = 31536000 seconds
Thus, it would take 137716666.667/31536000 = 4.367 years for light leaving Alpha Centauri to reach earth.
That means an image of Alpha Centauri viewed on earth today would be approximately 4.367 years old!
- You can only win for the first time on the 20th round, so you need to have lost 19 times before (2^19 = 524288, 2^20 = 1048576).
- The probability of losing 19 times in a row is 2^(-19) = 0.00000190734, or 0.00019073486%
- Given that it is quite likely that you will win on the first couple of rounds, I would not pay much to play the game. It is also unlikely that any casino would offer such a game due to the infinite expected value of winnings for the player.
Given that you may be able to win an infinitely large amount of money, you may believe it is fair to pay any fee that I request. This problem is usually referred to as the St. Petersburg paradox: although you are expected to win an infinite amount of money, you most likely won’t, so should therefore not pay a very large fee to enter the game.
You always make a profit of X, exactly doubling your initial bet!
So, what’s the catch? Well, the odds were in your favour in this game (2/3 to 1/3) which makes it more likely for you to win. In theory, this is a winning strategy if the odds are at least 50/50 (they never are at a casino), you have unlimited funds (good for you!) and there are no limits in bet size.
Disclaimer: we are not responsible if you decide to use this strategy and lose all your money.
One possible solution is to the right. Can you find any others? There are at least two different solutions!

You should find that you get closer to pi the more needles you drop.
You will (almost always) find that the circumference is much longer than the height of the glass. Most people find this to be very surprising!
This is the famous Monty Hall problem; there is a nice explanation of the solution on Wikipedia.
You can see an animation of the solution using Geogebra.
Minerva McGonagall = 49755941 4376516133
Minerva = 4 + 9 + 7 + 5 + 5 + 9 + 4 + 1 = 44
McGonagall = 4 + 3 + 7 + 6 + 5 + 1 + 6 + 1 + 3 + 3 = 39
Character number: 2 ( 44 + 39 = 83, 8 + 3 = 11, 1 + 1 = 2 )
Heart number: 5 (9 + 5 + 1 + 6 + 1 + 1 = 23, 2 + 3 = 5)
Social number: 6 ( 83 – 23 = 60 )
One way to do this is to work out how far the Lord travels between each of the servant's visits. However, there is a much slicker way:
Since the lord travels at 0.5 miles per hour, it will take him 2 hours until he reaches the Parliament.
The servant will be constantly moving during these two hours at a constant speed of 5 miles per hour. Therefore, he must have travelled a total of 10 miles.
Let's call the area A.
Picture 1: Depending on how you decide if a square is mostly inside the circle or not, there are between 4 and 16 squares, and the squares have area 1. So 4 \(\leq\) A \(\leq\) 16 (=4*1 and =16*1).
The other two pictures use a similar method:
Picture 2: 4 \(\leq\) A \(\leq\) 9 (=16*0.25 and =36*0.25)
Picture 3: 5.92 \(\leq\) A \(\leq\) 8.32 (=148*0.04 and =208*0.04) Using the formula A=pi*r2 with a radius of 1.5 gives A = 7.06858347058...
So the estimated areas are getting closer to the true area.
First must convert the height to metres:
1 ft \approx 0.3m, 1inch \approx 0.025m
5ft = 1.5m
7 inches = 0.175 m
Height = 1.675m
Now use the BMI formula to calculate the weight: 22.1*1.6752= 62kg
Now use the dosage formula to get the maximum allowable volume: 7*62/10*1/0.5=7*6.2*2= 86.8 mL
P(A) = probability that patient is disease free = 0.99
P(B) = probability that the test is positive = 0.10304
P(B|A) = probability of testing positive given that you don’t have the disease = 0.096
Now we calculate P(A|B) : the probability that the patient is disease free given they have received a positive test result using Bayes Theorem.
P(A|B)=P(B|A)P(A)/P(B) = 0.096*0.99/0.10304 = 0.9223602.
So, in this case, even though the patient has tested positive, there is an over 90% chance that they're disease-free!
They started at the North Pole.
There are a few ways to do this. For example:
- Start at the top right;
- Walk clockwise around the outside until you get back there;
- Now walk south-west to the middle bottom point (passing through the central point);
- Return to the central point on the curved path;
- Walk north-west to complete the remaining path.
If you remove the crossed-out path then it is no longer possible to complete the route. See Euler's Analysis for more information on this.
- The Union Canal is about 50km, and the soliton speed turns out to be 4.43m/s, which is about 10mph. So it would take about 11.3 hours, or approximately 11 hours and 20 minutes for the soliton to travel the length of the canal.
- This is much faster than you could walk it, by a factor of about 3.
- This is a pretty reasonable speed to cycle at.

