Scalar mixing

The mixing of scalars in a fluid is considerably accelerated by stirring. The stretching caused by the stirring leads to the formation of filamentary structures with sharp concentration contrasts and, as a result, to fast mixing by diffusion. Mathematical models of this process can be developed which represent fluid flows by random processes; these make it possible to understand the speed of the mixing, and other properties of the evolving constituent concentration. (with P H Haynes)

The figures illustrate the nature of the mixing by showing how the high (red) and low (blue) concentrations of a scalar in a disc evolve rapidly toward the mean value (white) when stirred by a random flow. Note how at early times (first 2 panels) the highs and lows of the concentration remain essentially unchanged. It is only at later times (last 2 panels) that diffusion acts efficiently to homogenise concentration. Note also that the flow vanishes at the boundary of the disc; stirring is relatively inefficient there, and the low (blue) concentrations remain persistent.

Steady two-dimensional flows

The colours represent the vorticity of a steady flow inside the domain with five-fold symmetry that is bounded by the thick black curve. The thin black lines are streamfunction contours. This flow is obtained by mapping the vorticity of a steady axisymmetric flow in disc on the non-axisymmetric domain in a manner which preserves steadiness (with D Wirosoetisno).

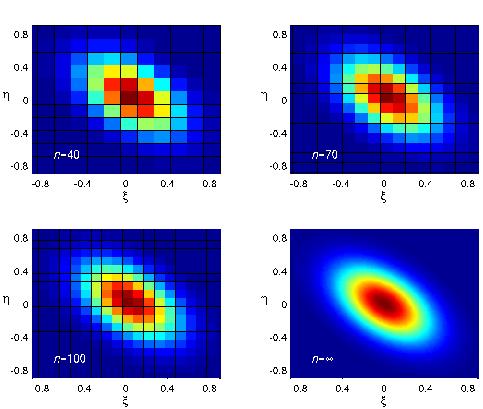
Asymptotics of a slow manifold

This shows the large n behaviour of some coefficients in an asymptotic expansion determining the slow manifold of the Lorenz 5-component model. This coefficients are defined for a discrete set of values of ξ and η which becomes dense as n → ∞.